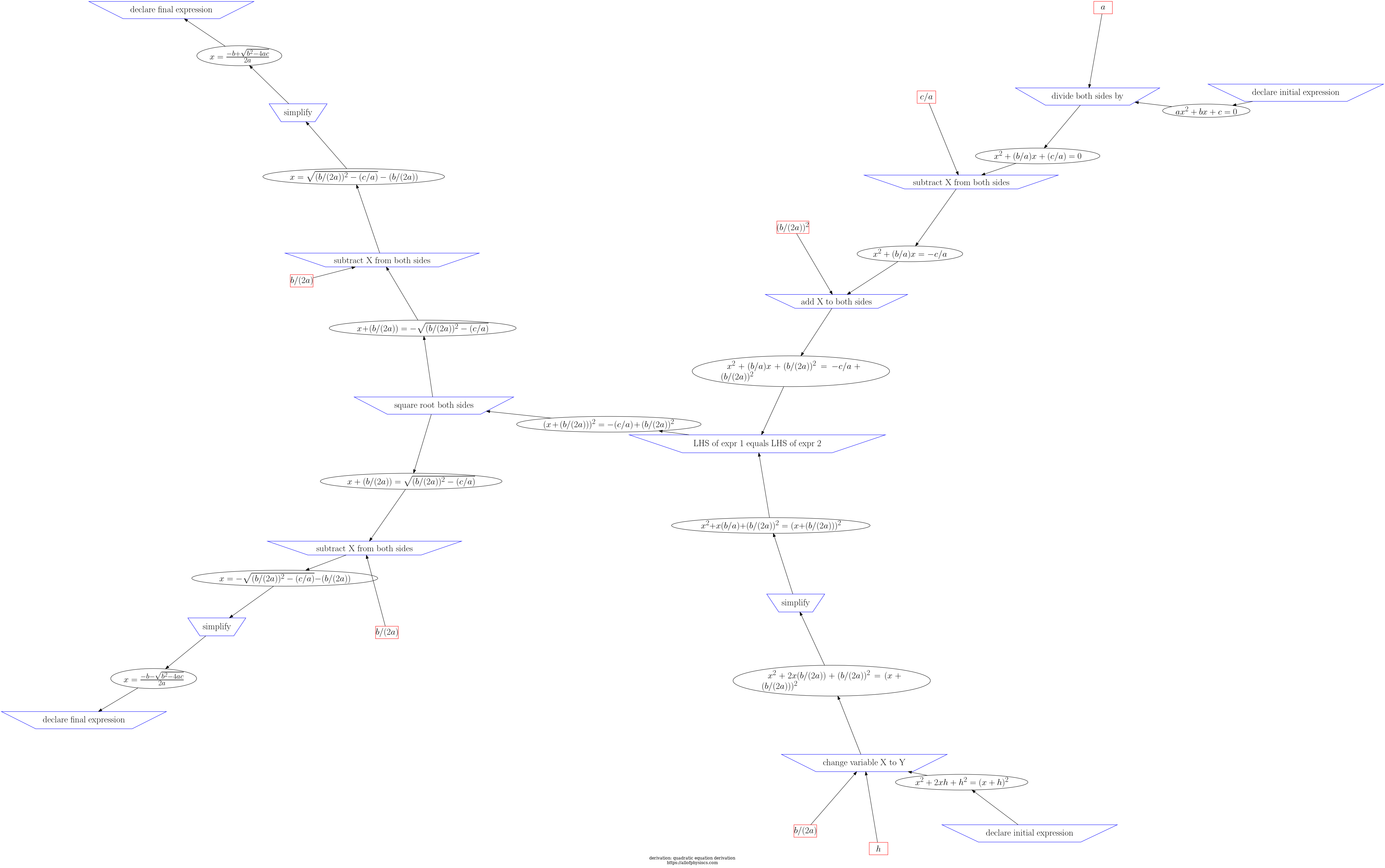
Welcome to the Physics Derivation Graph

Return to navigation page or list derivations

Review quadratic equation derivation

abstract:
reference: https://en.wikipedia.org/wiki/Quadratic_formula#Derivations_of_the_formula

step	inference rule	input	feed	output	validity (as per SymPy)
10	ID: 111282; subtract X from both sides number of inputs: 1; feeds: 1; outputs: 1 Subtract $#1$ from both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5982958249 $x+(b/(2 a))=-\sqrt{(b/(2 a))^2 - (c/a)}$	0002838490 $b/(2 a)$	9582958293 $x=\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))$	LHS diff is 0 RHS diff is -sqrt((pdg0001939*2 - 4pdg0004231pdg0009139)/pdg0009139*2)
10.5	ID: 111282; subtract X from both sides number of inputs: 1; feeds: 1; outputs: 1 Subtract $#1$ from both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9582958294 $x+(b/(2 a))=\sqrt{(b/(2 a))^2 - (c/a)}$	0002449291 $b/(2 a)$	5982958248 $x=-\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))$	LHS diff is 0 RHS diff is sqrt((pdg0001939*2 - 4pdg0004231pdg0009139)/pdg0009139*2)
11	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	5982958248 $x=-\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))$		9999999968 $x=\frac{-b-\sqrt{b^2-4ac}}{2 a}$	LHS diff is 0 RHS diff is (-pdg0009139sqrt((pdg00019392 - 4pdg0004231pdg0009139)/pdg00091392) + sqrt(pdg00019392 - 4pdg0004231pdg0009139))/(2pdg0009139)
11.5	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	9582958293 $x=\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))$		9999999969 $x=\frac{-b+\sqrt{b^2-4ac}}{2 a}$	LHS diff is 0 RHS diff is (pdg0009139sqrt((pdg00019392 - 4pdg0004231pdg0009139)/pdg00091392) - sqrt(pdg00019392 - 4pdg0004231pdg0009139))/(2pdg0009139)
5	ID: 111530; add X to both sides number of inputs: 1; feeds: 1; outputs: 1 Add $#1$ to both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5938459282 $x^2 + (b/a)x=-c/a$	0004307451 $(b/(2 a))^2$	5928292841 $x^2 + (b/a)x + (b/(2 a))^2=-c/a + (b/(2 a))^2$	valid
4	ID: 111282; subtract X from both sides number of inputs: 1; feeds: 1; outputs: 1 Subtract $#1$ from both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5958392859 $x^2 + (b/a)x+(c/a)=0$	0006644853 $c/a$	5938459282 $x^2 + (b/a)x=-c/a$	LHS diff is pdg0001464*(-pdg0001939 + pdg0009139)/pdg0009139 RHS diff is 0
9	ID: 111524; square root both sides number of inputs: 1; feeds: 0; outputs: 2 Take the square root of both sides of Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2} and Eq.~\\ref{eq:#3}.	9385938295 $(x+(b/(2 a)))^2=-(c/a) + (b/(2 a))^2$		9582958294 $x+(b/(2 a))=\sqrt{(b/(2 a))^2 - (c/a)}$ 5982958249 $x+(b/(2 a))=-\sqrt{(b/(2 a))^2 - (c/a)}$	recognized infrule but not yet supported
8	ID: 111355; LHS of expr 1 equals LHS of expr 2 number of inputs: 2; feeds: 0; outputs: 1 LHS of Eq.~\\ref{eq:#1} is equal to LHS of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5959282914 $x^2 + x(b/a) + (b/(2 a))^2=(x+(b/(2 a)))^2$ 5928292841 $x^2 + (b/a)x + (b/(2 a))^2=-c/a + (b/(2 a))^2$		9385938295 $(x+(b/(2 a)))^2=-(c/a) + (b/(2 a))^2$	valid
7	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	5928285821 $x^2 + 2 x (b/(2 a)) + (b/(2 a))^2=(x + (b/(2 a)))^2$		5959282914 $x^2 + x(b/a) + (b/(2 a))^2=(x+(b/(2 a)))^2$	valid
6	ID: 111886; change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.	8582954722 $x^2 + 2 x h + h^2=(x + h)^2$	0004858592 $h$ 0000999900 $b/(2 a)$	5928285821 $x^2 + 2 x (b/(2 a)) + (b/(2 a))^2=(x + (b/(2 a)))^2$	valid
14	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	9999999968 $x=\frac{-b-\sqrt{b^2-4ac}}{2 a}$			no validation is available for declarations
15	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	9999999969 $x=\frac{-b+\sqrt{b^2-4ac}}{2 a}$			no validation is available for declarations
3	ID: 111975; divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	9285928292 $ax^2 + bx + c=0$	0002424922 $a$	5958392859 $x^2 + (b/a)x+(c/a)=0$	Algebraic error: LHS diff is pdg0001464*(pdg0001939 - pdg0009139)/pdg0009139, RHS diff is 0
1	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			9285928292 $ax^2 + bx + c=0$	no validation is available for declarations
7.5	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8582954722 $x^2 + 2 x h + h^2=(x + h)^2$	no validation is available for declarations

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.005 seconds for pdg_app/to_review_derivation: node_properties, derivation1667069
0.02 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation2300162
0.011 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8463970
0.012 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8463970
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8463970
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8463970
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_sequence_index2300162
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2212814
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2212814
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2212814
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2212814
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2052240
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2052240
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2052240
0.021 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2052240
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8583494
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8583494
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8583494
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8583494
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7208227
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7208227
0.011 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7208227
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7208227
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8577201
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8577201
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8577201
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8577201
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4629179
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4629179
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4629179
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4629179
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6574464
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6574464
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6574464
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6574464
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8569354
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8569354
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8569354
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8569354
0.011 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9322564
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9322564
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9322564
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9322564
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9514667
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9514667
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9514667
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9514667
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3801149
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3801149
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3801149
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3801149
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1322564
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1322564
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1322564
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1322564
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6159879
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6159879
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6159879
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6159879
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6044997
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6044997
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6044997
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6044997
0.005 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation1667069
0.007 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id1667069000011
0.025 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule1667069
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9994803
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9994803
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9994803
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9994803
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7626678
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7626678
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7626678
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7626678
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2766880
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2766880
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2766880
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2766880
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5202467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5202467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5202467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5202467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1176894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1176894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1176894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1176894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1553901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1553901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1553901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1553901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7117829
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7117829
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7117829
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7117829
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9417781
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9417781
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9417781
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9417781
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7834430
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7834430
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7834430
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7834430
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8148598
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8148598
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8148598
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8148598
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9168304
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9168304
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9168304
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9168304
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7998393
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7998393
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7998393
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7998393
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6246480
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6246480
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6246480
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6246480
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4697523
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4697523
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4697523
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4697523
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7809487
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7809487
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7809487
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7809487
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9687901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9687901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9687901
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9687901
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8295080
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8295080
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8295080
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8295080
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5857689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5857689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5857689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5857689
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3556472
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3556472
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3556472
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3556472
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3062833
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3062833
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3062833
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3062833
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7090698
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7090698
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7090698
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7090698
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8675261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8675261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8675261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8675261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9485049
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9485049
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9485049
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9485049
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7409756
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7409756
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7409756
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7409756
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6210087
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6210087
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6210087
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6210087
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4098242
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4098242
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4098242
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4098242
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9864350
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9864350
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9864350
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9864350
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2891358
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2891358
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2891358
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2891358
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7571605
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7571605
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7571605
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7571605
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4356838
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4356838
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4356838
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4356838

step	inference rule	input	feed	output	validity (as per SymPy)
10	ID: 111282; subtract X from both sides number of inputs: 1; feeds: 1; outputs: 1 Subtract $#1$ from both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5982958249 \(x+(b/(2 a))=-\sqrt{(b/(2 a))^2 - (c/a)}\)	0002838490 \(b/(2 a)\)	9582958293 \(x=\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)	LHS diff is 0 RHS diff is -sqrt((pdg0001939*2 - 4pdg0004231pdg0009139)/pdg0009139*2)
10.5	ID: 111282; subtract X from both sides number of inputs: 1; feeds: 1; outputs: 1 Subtract $#1$ from both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9582958294 \(x+(b/(2 a))=\sqrt{(b/(2 a))^2 - (c/a)}\)	0002449291 \(b/(2 a)\)	5982958248 \(x=-\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)	LHS diff is 0 RHS diff is sqrt((pdg0001939*2 - 4pdg0004231pdg0009139)/pdg0009139*2)
11	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	5982958248 \(x=-\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)		9999999968 \(x=\frac{-b-\sqrt{b^2-4ac}}{2 a}\)	LHS diff is 0 RHS diff is (-pdg0009139sqrt((pdg00019392 - 4pdg0004231pdg0009139)/pdg00091392) + sqrt(pdg00019392 - 4pdg0004231pdg0009139))/(2pdg0009139)
11.5	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	9582958293 \(x=\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)		9999999969 \(x=\frac{-b+\sqrt{b^2-4ac}}{2 a}\)	LHS diff is 0 RHS diff is (pdg0009139sqrt((pdg00019392 - 4pdg0004231pdg0009139)/pdg00091392) - sqrt(pdg00019392 - 4pdg0004231pdg0009139))/(2pdg0009139)
5	ID: 111530; add X to both sides number of inputs: 1; feeds: 1; outputs: 1 Add $#1$ to both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5938459282 \(x^2 + (b/a)x=-c/a\)	0004307451 \((b/(2 a))^2\)	5928292841 \(x^2 + (b/a)x + (b/(2 a))^2=-c/a + (b/(2 a))^2\)	valid
4	ID: 111282; subtract X from both sides number of inputs: 1; feeds: 1; outputs: 1 Subtract $#1$ from both sides of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5958392859 \(x^2 + (b/a)x+(c/a)=0\)	0006644853 \(c/a\)	5938459282 \(x^2 + (b/a)x=-c/a\)	LHS diff is pdg0001464*(-pdg0001939 + pdg0009139)/pdg0009139 RHS diff is 0
9	ID: 111524; square root both sides number of inputs: 1; feeds: 0; outputs: 2 Take the square root of both sides of Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2} and Eq.~\\ref{eq:#3}.	9385938295 \((x+(b/(2 a)))^2=-(c/a) + (b/(2 a))^2\)		9582958294 \(x+(b/(2 a))=\sqrt{(b/(2 a))^2 - (c/a)}\) 5982958249 \(x+(b/(2 a))=-\sqrt{(b/(2 a))^2 - (c/a)}\)	recognized infrule but not yet supported
8	ID: 111355; LHS of expr 1 equals LHS of expr 2 number of inputs: 2; feeds: 0; outputs: 1 LHS of Eq.~\\ref{eq:#1} is equal to LHS of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5959282914 \(x^2 + x(b/a) + (b/(2 a))^2=(x+(b/(2 a)))^2\) 5928292841 \(x^2 + (b/a)x + (b/(2 a))^2=-c/a + (b/(2 a))^2\)		9385938295 \((x+(b/(2 a)))^2=-(c/a) + (b/(2 a))^2\)	valid
7	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	5928285821 \(x^2 + 2 x (b/(2 a)) + (b/(2 a))^2=(x + (b/(2 a)))^2\)		5959282914 \(x^2 + x(b/a) + (b/(2 a))^2=(x+(b/(2 a)))^2\)	valid
6	ID: 111886; change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.	8582954722 \(x^2 + 2 x h + h^2=(x + h)^2\)	0004858592 \(h\) 0000999900 \(b/(2 a)\)	5928285821 \(x^2 + 2 x (b/(2 a)) + (b/(2 a))^2=(x + (b/(2 a)))^2\)	valid
14	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	9999999968 \(x=\frac{-b-\sqrt{b^2-4ac}}{2 a}\)			no validation is available for declarations
15	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	9999999969 \(x=\frac{-b+\sqrt{b^2-4ac}}{2 a}\)			no validation is available for declarations
3	ID: 111975; divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	9285928292 \(ax^2 + bx + c=0\)	0002424922 \(a\)	5958392859 \(x^2 + (b/a)x+(c/a)=0\)	Algebraic error: LHS diff is pdg0001464*(pdg0001939 - pdg0009139)/pdg0009139, RHS diff is 0
1	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			9285928292 \(ax^2 + bx + c=0\)	no validation is available for declarations
7.5	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8582954722 \(x^2 + 2 x h + h^2=(x + h)^2\)	no validation is available for declarations