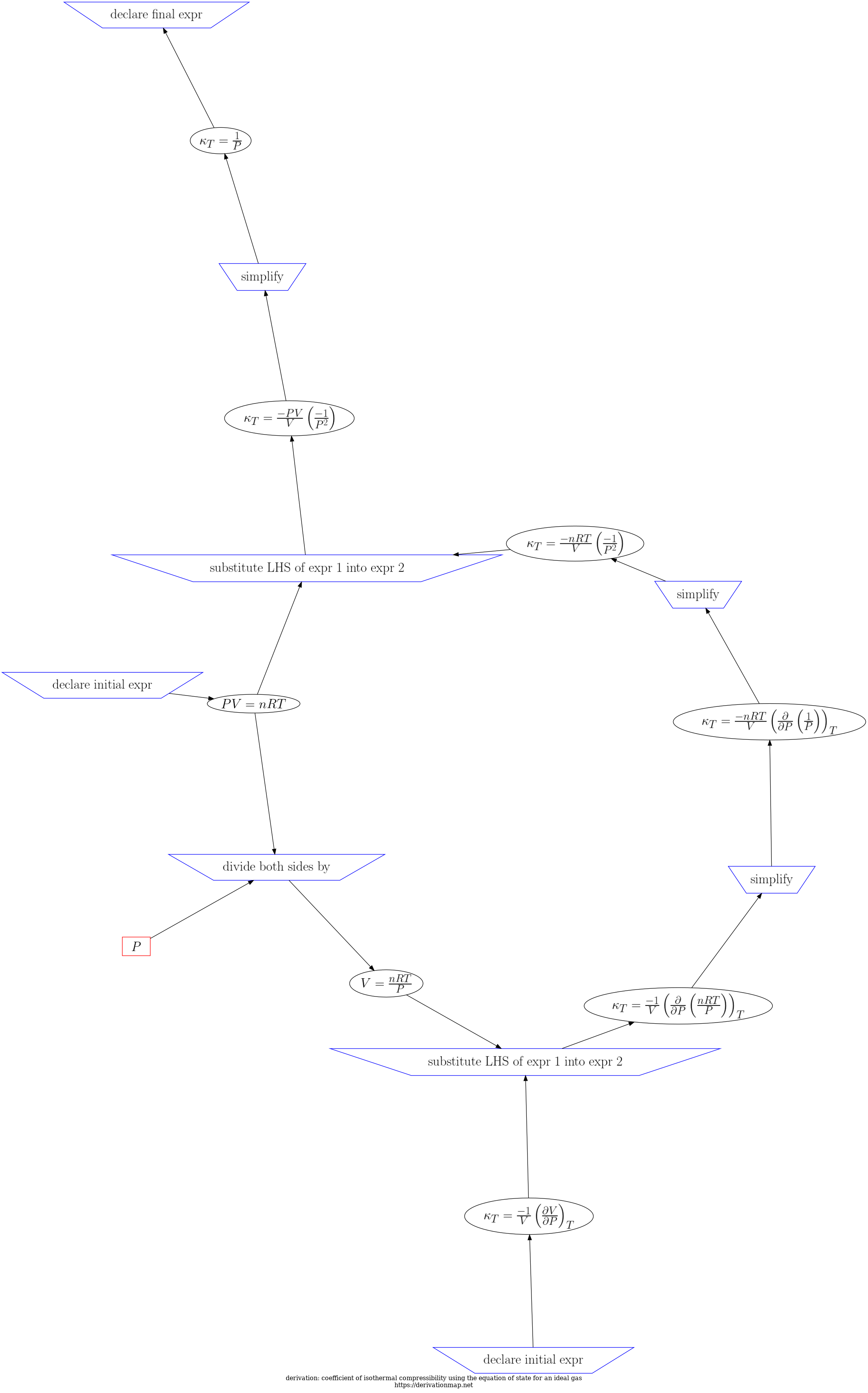
Physics Derivation Graph navigation Sign in

review derivation: coefficient of isothermal compressibility using the equation of state for an ideal gas

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
https://notendur.hi.is/hj/EE2/HD1lausn.pdf

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
9 declare final expr
  1. 9718685793; locally 2206759:
    \(\kappa_T = \frac{1}{P}\)
    \(pdg_{4645} = \frac{1}{pdg_{8134}}\)
no validation is available for declarations 9718685793:
9718685793:
6 simplify
  1. 1190768176; locally 3915956:
    \(\kappa_T = \frac{-nRT}{V} \left( \frac{ \partial }{\partial P}\left(\frac{1}{P}\right) \right)_T\)
    \(pdg_{4645} = - \frac{pdg_{2834} pdg_{7343} pdg_{8179} \frac{d}{d pdg_{8134}} \frac{1}{pdg_{8134}}}{pdg_{7586}}\)
  1. 3605073197; locally 6275836:
    \(\kappa_T = \frac{-nRT}{V} \left( \frac{-1}{P^2}\right)\)
    \(pdg_{4645} = \frac{pdg_{2834} pdg_{7343} pdg_{8179}}{pdg_{7586} pdg_{8134}^{2}}\)
valid 1190768176:
3605073197:
1190768176:
3605073197:
1 declare initial expr
  1. 9781951738; locally 4239912:
    \(\kappa_T = \frac{-1}{V} \left( \frac{ \partial V}{\partial P} \right)_T\)
    \(pdg_{4645} = - \frac{\frac{d}{d pdg_{8134}} pdg_{7586}}{pdg_{7586}}\)
no validation is available for declarations 9781951738:
9781951738:
3 divide both sides by
  1. 8435841627; locally 4454896:
    \(P V = n R T\)
    \(pdg_{7586} pdg_{8134} = pdg_{2834} pdg_{7343} pdg_{8179}\)
  1. 6296166842:
    \(P\)
    \(pdg_{8134}\)
  1. 3497828859; locally 5840241:
    \(V = \frac{n R T}{P}\)
    \(pdg_{7586} = \frac{pdg_{2834} pdg_{7343} pdg_{8179}}{pdg_{8134}}\)
valid 8435841627: inconsistent dimensions
3497828859:
8435841627: N/A
3497828859:
7 substitute LHS of expr 1 into expr 2
  1. 8435841627; locally 4454896:
    \(P V = n R T\)
    \(pdg_{7586} pdg_{8134} = pdg_{2834} pdg_{7343} pdg_{8179}\)
  2. 3605073197; locally 6275836:
    \(\kappa_T = \frac{-nRT}{V} \left( \frac{-1}{P^2}\right)\)
    \(pdg_{4645} = \frac{pdg_{2834} pdg_{7343} pdg_{8179}}{pdg_{7586} pdg_{8134}^{2}}\)
  1. 9847143017; locally 1003658:
    \(\kappa_T = \frac{-PV}{V} \left( \frac{-1}{P^2}\right)\)
    \(pdg_{4645} = \frac{1}{pdg_{8134}}\)
valid 8435841627: inconsistent dimensions
3605073197:
9847143017:
8435841627: N/A
3605073197:
9847143017:
5 simplify
  1. 8368984890; locally 5196207:
    \(\kappa_T = \frac{-1}{V} \left( \frac{ \partial }{\partial P}\left(\frac{nRT}{P}\right) \right)_T\)
    \(pdg_{4645} = - \frac{\frac{\partial}{\partial pdg_{8134}} \frac{pdg_{2834} pdg_{7343} pdg_{8179}}{pdg_{8134}}}{pdg_{7586}}\)
  1. 1190768176; locally 3915956:
    \(\kappa_T = \frac{-nRT}{V} \left( \frac{ \partial }{\partial P}\left(\frac{1}{P}\right) \right)_T\)
    \(pdg_{4645} = - \frac{pdg_{2834} pdg_{7343} pdg_{8179} \frac{d}{d pdg_{8134}} \frac{1}{pdg_{8134}}}{pdg_{7586}}\)
valid 8368984890:
1190768176:
8368984890:
1190768176:
8 simplify
  1. 9847143017; locally 1003658:
    \(\kappa_T = \frac{-PV}{V} \left( \frac{-1}{P^2}\right)\)
    \(pdg_{4645} = \frac{1}{pdg_{8134}}\)
  1. 9718685793; locally 2206759:
    \(\kappa_T = \frac{1}{P}\)
    \(pdg_{4645} = \frac{1}{pdg_{8134}}\)
valid 9847143017:
9718685793:
9847143017:
9718685793:
4 substitute LHS of expr 1 into expr 2
  1. 3497828859; locally 5840241:
    \(V = \frac{n R T}{P}\)
    \(pdg_{7586} = \frac{pdg_{2834} pdg_{7343} pdg_{8179}}{pdg_{8134}}\)
  2. 9781951738; locally 4239912:
    \(\kappa_T = \frac{-1}{V} \left( \frac{ \partial V}{\partial P} \right)_T\)
    \(pdg_{4645} = - \frac{\frac{d}{d pdg_{8134}} pdg_{7586}}{pdg_{7586}}\)
  1. 8368984890; locally 5196207:
    \(\kappa_T = \frac{-1}{V} \left( \frac{ \partial }{\partial P}\left(\frac{nRT}{P}\right) \right)_T\)
    \(pdg_{4645} = - \frac{\frac{\partial}{\partial pdg_{8134}} \frac{pdg_{2834} pdg_{7343} pdg_{8179}}{pdg_{8134}}}{pdg_{7586}}\)
LHS diff is 0 RHS diff is -(pdg2834*pdg7343*pdg8179 - pdg7586*pdg8134)/(pdg7586*pdg8134**2) 3497828859:
9781951738:
8368984890:
3497828859:
9781951738:
8368984890:
2 declare initial expr
  1. 8435841627; locally 4454896:
    \(P V = n R T\)
    \(pdg_{7586} pdg_{8134} = pdg_{2834} pdg_{7343} pdg_{8179}\)
no validation is available for declarations 8435841627: inconsistent dimensions
 8435841627: N/A
Physics Derivation Graph: Steps for coefficient of isothermal compressibility using the equation of state for an ideal gas

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
7586 variable V
\(V\)		 real
  • length: 3
 volume 15
8134 variable P
\(P\)		 real
  • length: -1
  • mass: 1
  • time: -2
 pressure 13
4645 variable \kappa_T
\(\kappa_T\)		 real dimensionless coefficient of isothermal compressibility
  • str_note
6
7343 variable T
\(T\)		 real
  • temperature: 1
 temperature 18
2834 variable n
\(n\)		 real dimensionless amount of substance 8
8179 constant R
\(R\)		 real
  • amount of substance: -1
  • length: 2
  • mass: 1
  • temperature: -1
  • time: -2
 ideal gas constant 8.31446261815324   Jā‹…K^{āˆ’1} mol^{āˆ’1}
 8
MESSAGE: