This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
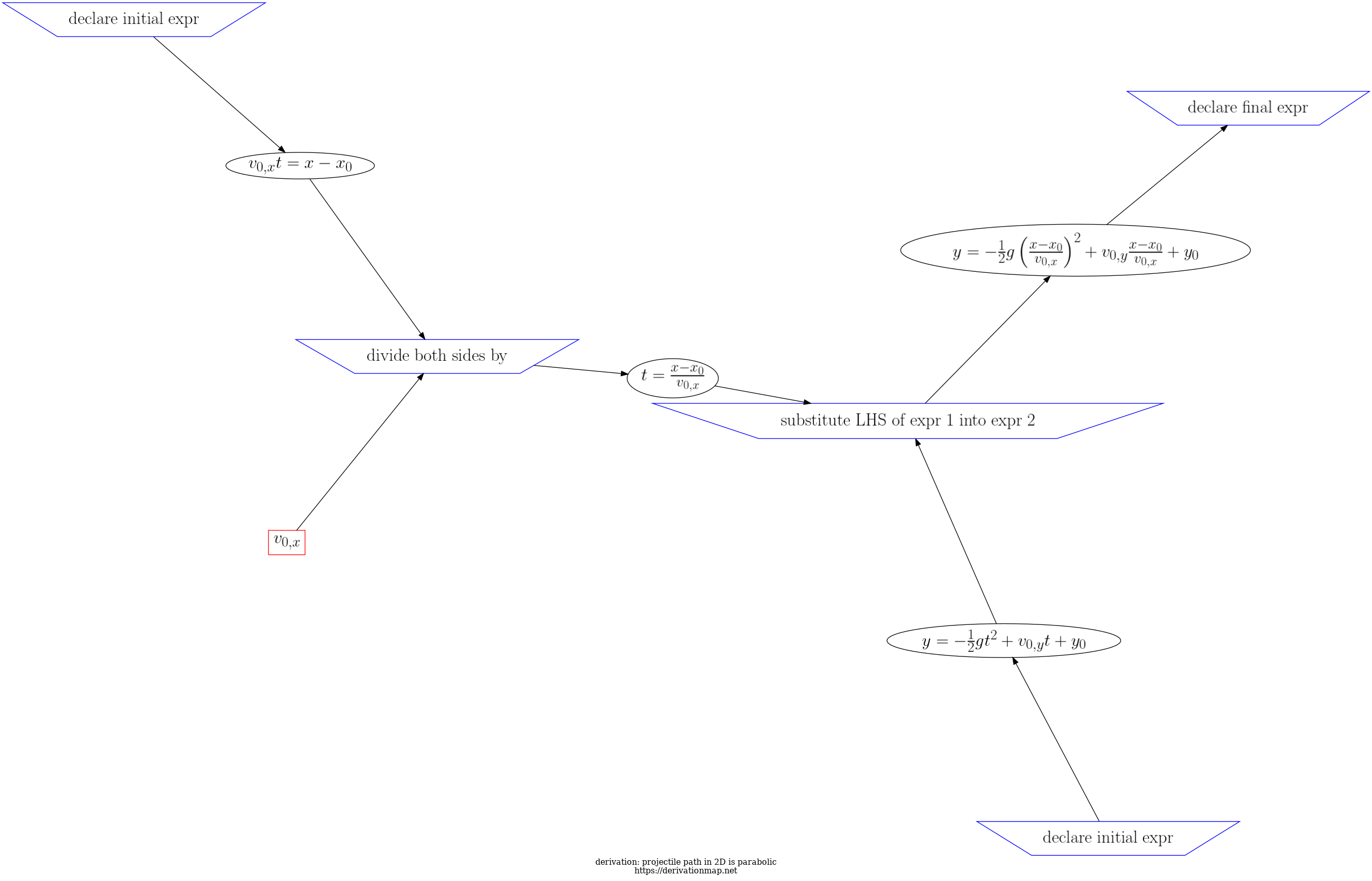
Using the 2D equations of motion, show that projectile path is second order polynomial of the form y = a x^2 + b x + c
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 4 | substitute LHS of expr 1 into expr 2 |
|
|
|
LHS diff is 0 RHS diff is (pdg1572 - pdg4037)*(pdg1649*(pdg1572 - pdg4037)*(pdg1649 - 1) + 2*pdg2958*(-pdg9107 + pdg9431))/(2*pdg2958**2) |
3274926090:
1405465835: dimensions are consistent 7354529102: |
3274926090:
1405465835: N/A 7354529102: |
|
| 2 | divide both sides by |
|
|
|
valid |
9882526611:
3274926090: |
9882526611:
3274926090: |
|
| 5 | declare final expr |
|
|
|
no validation is available for declarations |
7354529102:
|
7354529102:
|
expression is a second order polynomial; projecticle motion is parabolic |
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
9882526611:
|
9882526611:
|
|
| 3 | declare initial expr |
|
|
|
no validation is available for declarations |
1405465835:
dimensions are consistent |
1405465835:
N/A |